La
serie de Fourier para señales discretas (sfsd)
El análisis para la
representación de
señales periódicas discretas en el dominio de la frecuencia resulta muy similar
al empleado para las señales periódicas de
tiempo continuo. La diferencia más importante radica en que la representación en
serie de Fourier de una señal discreta es una serie finita, en oposición al caso
de las señales periódicas continuas que requieren de una serie infinita.
La exponencial compleja
discreta, ej(2p
/N)n, es periódica con período N. además el conjunto de
total de las señales exponenciales complejas discretas que son periódicas con
período N está dado por:
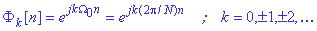
En este conjunto solo hay N
señales distintas, esto como consecuencia del hecho de que las exponenciales
complejas discretas que difieren en frecuencia por un múltiplo de 2p
son idénticas (a diferencia de las exponenciales complejas de tiempo continuo
que son todas diferentes):
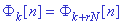
Definido este conjunto de
exponenciales complejas, se puede entonces hallar la representación de Fourier
para una señal periódica discreta, con período N
y frecuencia fundamental W0 = 2p/N
, mediante las ecuaciones:
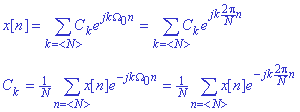
Estas ecuaciones
especifican una descomposición de x[n] en una suma de N exponenciales
complejas relacionadas armónicamente, de ahí la existencia entonces de N
valores para Ck (Ck=Ck+N ), dando origen a
un espectro discreto periódico.
Finalmente, para indicar la
correspondencia entre una señal periódica x[n] y sus coeficientes Ck
se utiliza la siguiente notación:
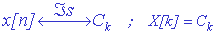
Para facilitar el cálculo
de estos coeficientes se debe aprovechar cualquier simetría presentada por
la señal x[n] y una adecuada escogencia del intervalo de n para los N
términos a utilizar en la sumatoria respectiva.
