La
serie de Fourier (sf)
Inicialmente el análisis de
señales en el dominio de la frecuencia se enfoca hacia las señales periódicas de
tiempo continuo. La representación de estas señales, en el dominio de la
frecuencia, se logra utilizando para ello el conjunto ortogonal de señales
conformado por las senoidales complejas (exponenciales) cuyas frecuencias son
múltiplos enteros de una frecuencia fundamental, esto es:

Esta serie, conocida como
serie exponencial de Fourier, es una forma muy conveniente de representar una
señal x(t) en el domino de la frecuencia, ya que mediante sus coeficientes se
obtienen:
Finalmente, para indicar la
correspondencia entre una señal periódica x(t) y sus coeficientes Cn
se utiliza la siguiente notación:
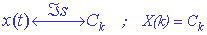
El
cálculo de estos coeficientes se facilita si la señal x(t) es real y posee
algún tipo de simetría. En estos casos es aplicable la Serie Trigonométrica
de Fourier, cuyos coeficientes son calculados aprovechando estas
características de simetría. Para la obtención de la serie trigonométrica de
Fourier se hace uso de las relaciones:
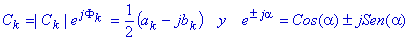
De este modo se obtiene una
nueva expresión para la señal x(t):
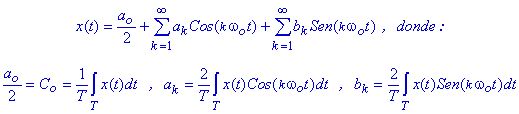
Esta serie trigonométrica
también se puede escribir en forma condensada:
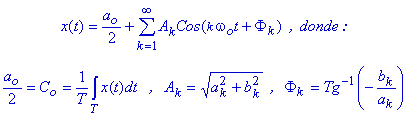

condiciones de simetría
para la señal x(t)
La existencia de simetría en la
señal x(t) permite simplificar el cálculo de los coeficientes de la serie
trigonométrica de Fourier. A continuación se resumen dichas condiciones de
simetría ya las respectivas ecuaciones para el calculo de los coeficientes.


Obtención
de una señal real x(t)
en el dominio w
Para la obtención de una señal
real x(t) en el dominio de la frecuencia se recomienda seguir los siguientes
pasos:
-
Evaluar la simetría de
x(t).
-
Si existe algún tipo de
simetría, calcular ak y bk.
-
Calcular Ck
y Fk.

Además, existen las siguientes relaciones entre los
coeficientes de las formas trigonométricas y la forma exponencial de la
serie de Fourier:
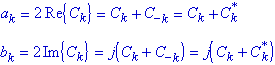
-
Dibujar el espectro
discreto obtenido:
Espectro de Amplitud: ...... |Ck| ............. Simetría Par.
Espectro de Fase: ..............arg|Ck| ....... Simetría Impar.