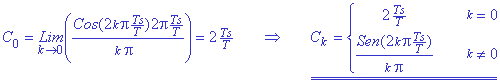Determine los coeficientes de la serie de Fourier para la
onda periódica cuadrada, mostrada en la figura y definida sobre un período como:
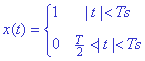
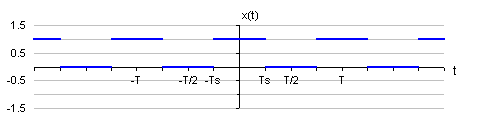
Esta señal, muy usada en el análisis de señales y sistemas,
es periódica con período fundamental T y con frecuencia fundamental
w0=2p/T.
Respuesta:
La señal x(t) presenta simetría
par, por lo que resulta conveniente calcular los coeficientes de la serie
trigonométrica de Fourier (ak y bk) , para luego calcular
los correspondientes valores para los coeficientes de la serie exponencial de
Fourier (Ck). Esta simetría par indica que:
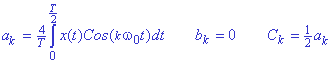
Así, con
w0=2p/T
se obtiene:
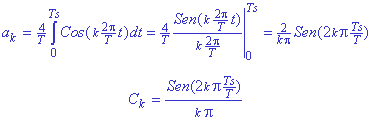
Esta expresión para Ck
está indeterminada para k=0, pero utilizando la regla de L'Hopital se obtiene su
valor:
Envíe un mensaje a