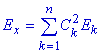Aquí se considera la representación de una señal como una superposición ponderada de senoides complejas. Si una señal de este tipo se aplica a un sistema lineal, entonces la salida del sistema es una superposición ponderada de la respuesta del sistema a cada senoide compleja.

Esta representación no solo conduce a una representación útil para la salida del sistema sino que también brinda una caracterización muy profunda de señales y sistemas, razón por la cual este enfoque se extiende al estudio de las propiedades de dichas representaciones.

El estudio de señales y sistemas empleando representaciones senoidales se denomina análisis de Fourier, en honor a Joseph Fourier (1768  - 1830) por sus contribuciones a la teoría de representación de funciones como superposiciones ponderadas de senoides. Los métodos de Fourier tienen una representación muy amplia más allá de las señales y los sistemas; se usan en todas las ramas de la ingeniería y la ciencia.

Senoides complejas y sistemas

Para un sistema lineal invariante en el tiempo (LTI), se ha demostrado que una entrada senoidal compleja genera una salida igual a la entrada senoidal multiplicada por la respuesta en frecuencia del sistema, lo cual en tiempo continuo se traduce en:

Donde la respuesta en frecuencia H(jw ) se define en términos de la respuesta al impulso h(t) como:

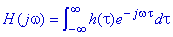
Representando las señales arbitrarias como superposiciones ponderadas de funciones características del sistema (como las funciones senoidales complejas, en el caso de un sistema LTI), se transforma la operación de convolución en una de multiplicación. Para ilustrar esto se expresa la entrada x(t) de un sistema LTI como la suma ponderada de M senoides complejas, obteniendo la salida y(t) respectiva:

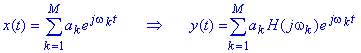
La salida es una suma ponderada de M senoides complejas, con los pesos, a_k, modificados por la respuesta en frecuencia del sistema, H(jw_k). Las operaciones de convolución, h(t) * x(t), se vuelven multiplicación, a_kH(jw_k). Este hecho es una motivación poderosa para representar señales como superposiciones ponderadas de senoides complejas. Además, los pesos brindan una interpretación alternativa de la señal. En lugar de describir el comportamiento de la señal como una función del tiempo, los pesos describen la señal como una función de la frecuencia, donde el peso asociado con una senoide de una frecuencia determinada representa la contribución de esta senoide a la señal completa, lo cual hace que una vista de una señal en el domino de la frecuencia sea muy informativa.

Ortogonalidad de senoides complejas

La ortogonalidad de las senoides complejas desempeña un papel fundamental en las representaciones de Fourier. De acuerdo a esto, esta sería la representación de una señal en un intervalo (T₁,T₂) por medio de señales ortogonales:

Si 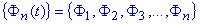es un conjunto de 'n' señales ortogonales en el intervalo (T₁,T₂) entonces podemos representar una señal x(t) en dicho intervalo como:

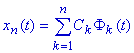
Donde los coeficientes, conocidos como coeficientes de Fourier, son:

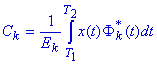
Obteniéndose además una expresión para la energía de la señal en términos de la energía de cada una de las señales de este conjunto ortogonal (Densidad Espectral de Energía):