FENÓMENOS DE TRANSPORTE

UNIDAD IV
CONTENIDO

TRANSFERENCIA DE CALOR

TRANSFERENCIA DE CALOR     Las leyes de la Termodinámica tratan de la transferencia de energía pero solo se refieren a sistemas que están en equilibrio. Por ello, permiten determinar la cantidad de energía requerida para cambiar un sistema de un estado de equilibrio a otro pero no sirven para predecir la rapidez con que puedan producirse estos cambios. La transferencia de calor complementa la primera y la segunda ley, proporcionando los métodos de análisis que pueden utilizarse para predecir esta velocidad de transmisión. Ejemplo: Calentamiento de una barra de acero colocada en agua caliente: Con la Termodinámica se predicen las temperaturas finales una vez los dos sistemas hayan alcanzado el equilibrio y la cantidad de energía transferida entre los dos estados de equilibrio inicial y final. Con la Transferencia de Calor se puede predecir la velocidad de transferencia térmica del agua a la barra así como la temperatura del agua en función del tiempo.     La Transferencia de Calor puede ser por conducción, convección y radiación. TRANSFERENCIA DE CALOR POR CONDUCCIÓN         Cuando en un medio sólido existe un gradiente de temperatura, el calor se transmite de la región de mayor temperatura a la de menor temperatura. El calor transmitido por conducción por unidad de tiempo qk es proporcional al gradiente de temperatura dT/dx multiplicado por el área A a través del cual se transfiere es decir                                              T: temperatura  ;  x:  dirección del flujo de calor El flujo de calor depende de la conductividad térmica k que es la propiedad física del medio [W/m K], luego se tiene                                                                                       Convenios del signo     Fig. 4.13 Representación del convenio del signo CONDUCCIÓN A TRAVÉS DE UNA PARED PLANA         El calor fluye en dirección perpendicular a la superficie. Si la conductividad térmica es uniforme, la integración de la ecuación queda como                                                                                    Fig. 4.14 Sección transversal de una pared plana CONDUCCIÓN A TRAVÉS DE PAREDES PLANAS EN SERIE      En estado estacionario el flujo de calor a través de todas las secciones debe ser el mismo. Sin embargo, los gradientes son distintos  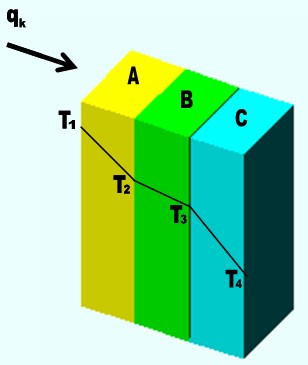                                                                                                                           Fig. 4.15 Conducción unidimensional a través de paredes planas en serie A partir de la ecuación 4.4 se tienen las siguientes relaciones                                                                                              sustituyendo 4.5 y 4.6 en 4.4                                                     luego el flujo de calor será                                                       Para un conjunto de n  paredes en perfecto contacto térmico, el flujo de calor es                  ANALOGÍA ELÉCTRICA DE LA CONDUCCIÓN         Utiliza los conceptos desarrollados en la teoría de los circuitos eléctricos y con frecuencia se llama analogía entre el flujo de calor y la electricidad. La combinación L/kA  equivale a una resistencia y la diferencia de temperatura es análoga a una diferencia de potencial. La ecuación puede escribirse en una forma semejante a la ley de Ohm de la teoría de los circuitos eléctricos                                                en donde                                                             El recíproco de la resistencia térmica se denomina conductancia térmica Para tres secciones en serie                                      MATERIALES DISPUESTOS EN PARALELO         El análisis del circuito supone que el flujo es unidimensional      Fig. 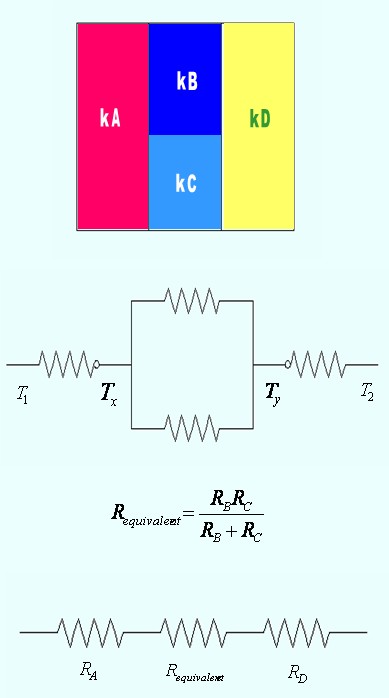4.16  Analogía eléctrica para paredes en paralelo                                                                               Fig. 4.17 Resistencia equivalente RESISTENCIA DE CONTACTO         Cuando superficies conductoras distintas se sitúan en contacto, aparece generalmente una resistencia térmica en la interfase de los sólidos. Esta resistencia, llamada resistencia de contacto, se desarrolla cuando los dos materiales no se ajustan exactamente y por ello entre ambos queda atrapada una delgada capa de fluido. A través de los puntos de contacto del sólido, el calor se transmite por conducción mientras que a través del fluido de la interfase el calor se transmite por convección y radiación. CONDUCTIVIDAD TÉRMICA         La conductividad térmica de un material varía con la temperatura. Los gases tienen conductividad térmica mas baja que los líquidos. Los metales como el cobre y el aluminio tienen conductividad térmica alta. TRANSFERENCIA DE CALOR POR CONVECCIÓN          Cuando un fluido se pone en contacto con una superficie sólida a una temperatura distinta, el proceso resultante de intercambio de energía térmica se denomina transferencia de calor por convección. Hay dos tipos de procesos de convección: convección libre o natural y convección forzada.          En el primer caso la fuerza motriz procede de la diferencia de densidad en el fluido que resulta del contacto con una superficie a diferente temperatura y da lugar a fuerzas ascensionales. En el segundo caso una fuerza motriz exterior mueve un fluido sobre una superficie a una temperatura mayor o inferior que la del fluido. Para una u otra forma de transferencia de calor por convección, la cantidad de calor es    Donde transferencia de calor por convección en la interfase líquido-sólido. A     área superficial en contacto con el fluido  en m2 Ts     Temperatura de la superficie , K Tf, ¥     Temperatura del fluido no perturbado lejos de la superficie transmisora del calor El coeficiente de transferencia de calor por convección depende de la densidad, viscosidad y velocidad del fluido, así como de sus propiedades térmicas (conductividad térmica y calor específico). La resistencia térmica en la transferencia de calor por convección viene dada por                                                      Fig. 4.18  Analogía eléctrica para la convección TRANSFERENCIA DE CALOR POR RADIACION         Por radiación la energía se transporta en forma de ondas electromagnéticas que se propagan a la velocidad de la luz. La radiación electromagnética que se considera aquí es la radiación térmica.         La cantidad de energía que abandona una superficie en forma de calor radiante depende de la temperatura absoluta y de la naturaleza de la superficie. Un radiador perfecto o cuerpo negro emite una cantidad de energía radiante de su superficie por unidad de tiempo qr dada por la ecuación                                                Para evaluar la transferencia neta de energía radiante requiere una diferencia en la temperatura superficial de dos o mas cuerpos entre los cuales tiene lugar el intercambio. Si un cuerpo negro irradia  a un recinto que lo rodea completamente y cuya superficie es también negra (es decir absorbe toda la energía radiante que incide sobre él, la transferencia neta de energía radiante por unidad de tiempo viene dada por     T1: Temperatura del cuerpo negro en Kelvin T2: Temperatura superficial del recinto en Kelvin Si a una temperatura igual a la de un cuerpo negro emiten una fracción constante de la emisión del cuerpo negro para cada longitud de onda, se llaman cuerpos grises. Un cuerpo gris emite radiación según la expresión     El calor radiante neto transferido por unidad de tiempo por un cuerpo gris a la temperatura T1 a un cuerpo negro que le rodea a la temperatura T2 es                                                                 donde e 1 es la emitancia de la superficie gris, igual a la relación entre la emisión de la superficie gris y la emisión de un radiador perfecto a la misma temperatura. Si ninguno de los dos cuerpos es un radiador perfecto, pero poseen entre sí una determinada relación geométrica, el calor radiante neto transferido entre ellos viene dado por           donde F1-2 es un módulo que modifica la ecuación de los radiadores perfectos para tener en cuenta las emitancias y las geometrías relativas de los cuerpos reales. ECUACIÓN DE LA CONDUCCIÓN                                           1) Cantidad neta de calor que entra en el volumen de control por conducción en la unidad de tiempo y por unidad de volumen. 2) Cantidad de energía generada en la unidad de tiempo y por unidad de volumen en el interior del volumen de control. 3) Aumento de la energía interna en la unidad de tiempo en el interior del volumen de control. La ecuación se puede expresar como        donde a  es la difusividad térmica y se expresa como      En coordenadas cilíndricas:  T=T(r, f ,z,t) En coordenadas esféricas: T=T(r, q , f ,t)                         FLUJO DE CALOR A TRAVÉS DE UN CILINDRO HUECO              Fig. 4.19 Calor por conducción en un cilindro hueco. Consideraciones: La distribución de temperaturas es función únicamente de r  T=T( r ) k es constante q,,,G      es igual a cero luego para las condiciones de frontera se tiene: De la ecuación de conducción  (4.27)   si se sustituyen las condiciones de frontera se obtienen dos ecuaciones resolviendo se consigue                                                                                   Una vez conocida la distribución de temperaturas, con la ley de Fourier en coordenadas cilíndricas, se determina la transferencia de calor                         El denominador de esta ecuación corresponde a la resistencia térmica FLUJO DE CALOR A TRAVÉS DE UNA ESFERA HUECA         Se considera flujo estable en la dirección r y la ecuación 4.28 quedaría expresada como                                                                   Esta expresión se puede escribir como Fig. 4.20. Calor por conducción en una esfera hueca Consideraciones: La distribución de temperaturas es función únicamente de r   T=T( r ) k es constante q,,,G    es igual a cero luego para las condiciones de frontera se tiene: de la ecuación 4.34 se tiene que 1/r no puede ser cero, luego      integrando nuevamente la ecuación 4.36      resolviendo para las condiciones de frontera, se tiene la siguiente expresión para la distribución de temperaturas           Una vez conocida la distribución de temperaturas con la ley de Fourier se determina la transferencia de calor                                    COEFICENTE GLOBAL DE TRANSFERENCIA DE CALOR         Cuando en un problema de transferencia intervienen varias resistencias térmicas en serie, en paralelo, o en combinación de ambas formas, es conveniente definir un coeficiente de transferencia de calor global o conductancia global.                                     TRANSFERENCIA DE CALOR POR CONVECCIÓN         La transferencia de calor por convección de un cuerpo comprende el movimiento de un fluido (líquido o gas) en relación con el cuerpo. CONVECCIÓN NATURAL         Ocurre debido a diferencias de densidad en el fluido provocadas por un cuerpo a una temperatura diferente que la del fluido que intercambia calor  con él. Estas diferencias de densidad provocan una acción de bombeo del fluido con relación al cuerpo. DETERMINACION DEL COEFICIENTE DE TRANSFERENCIA DE CALOR POR COVECCIÓN NATURAL         La evaluación del coeficiente de transferencia de calor h es bastante difícil puesto que por lo regular comprende fenómenos físicos muy complejos. Usando las técnicas del análisis dimensional puede demostrarse que los parámetros comprendidos en la transferencia de calor por convección natural pueden expresarse según                                     donde En esta ecuaciones las variables son A,a,b :  constantes dependientes del sistema en consideración   b  :        coeficiente de expansión r  :          densidad m  :        viscosidad g :        aceleración de la gravedad D :       diámetro L :        longitud Cp :      Calor específico a presión constante La capa límite del fluido será laminar o turbulenta y esto a su vez afectará las constantes de la ecuación 4.41. Para calcular el coeficiente de transferencia de calor por convección natural, se usa: (Tablas   1 ,   2   ,   3   ). La tabla 1 se usa para determinar primero si el carácter del flujo es laminar o turbulento. Los datos necesarios para tener acceso a esta gráfica son D t y L (o D). Una vez determinado el carácter del flujo, se utilizan las tablas 2 y 3 para calcular el coeficiente de transferencia de calor por convección. CONVECCIÓN  FORZADA        El flujo de convección forzada puede ser laminar o turbulento, interior o exterior a la tubería e involucrar cambios de fase tales como cuando un fluido está calentándose. Solo se estudiará la situación en la que se tenga un líquido o un gas que fluye en el interior de un tubo en un flujo turbulento. DETERMINACIÓN DEL COEFICIENTE DE TRANSFERENCIA DE CALOR POR CONVECCIÓN FORZADA      Las tablas ( 4  ,   5   ): Dan la viscosidad del agua y el aire y se usan para verificar el número de Reynolds y asegurar que el flujo es turbulento.      Las tablas ( 6  ,   7   ): Conducen al coeficiente de transferencia de calor básico  h1 como función del flujo en peso W/1000, donde W está en libras por hora.      La tabla (   8   ): Es un factor de corrección para la variación del diámetro interior desde 1 pulgada. El coeficiente de transferencia de calor buscado h es entonces simplemente igual  a  F.h1 TRANSFERENCIA DE CALOR POR RADIACIÓN        La transmisión de calor por radiación se caracteriza porque la energía se transporta en forma de ondas electromagnéticas, que se propagan a la velocidad de la luz. El transporte de energía por radiación puede verificarse entre superficies separadas por el vacío. El sol por ejemplo, transmite energía a la Tierra enteramente por radiación a través de millones de kilómetros de espacio vacío.        Un cuerpo negro se define como aquel que emite y absorbe la máxima cantidad de energía a una temperatura determinada.        Los cuerpos reales reflejan radiación térmica en la misma forma en que la absorben y la transmiten. Los metales muy pulidos son buenos reflectores de la radiación térmica. Reflectividad: r  Es la fracción de calor incidente sobre el cuerpo que se refleja. Absortividad: a   Es la fracción que se absorbe. Transmisividad: t  Es la fracción de energía incidente transmitida a través del cuerpo. Emisividad: e  Es la efectividad del cuerpo como un radiador térmico a una temperatura. Es la relación de la emisión de calor a una temperatura dada a la emisión de calor desde un cuerpo negro a la misma temperatura. INTERCAMBIO NETO DE CALOR POR RADIACIÓN ENTRE DOS CUERPOS A DIFERENTES TEMPERATURAS         Para calcular esta transferencia de calor se puede escribir       En las tablas: (   9  ,   10   ,   11   ,   12  ,   13   ) se dan los valores requeridos de Fe y FA para lo cual es necesario conocer la emisividad de las superficies que intervienen. INTERCAMBIADORES DE CALOR         Los intercambiadores están  diseñados para realizar una función específica. Las plantas de generación a vapor usan condensadores, economizadores, calentadores de agua de alimentación, recalentadores, etc. En los intercambiadores la temperatura de uno o ambos fluidos varía en forma continua a medida que los fluidos se transportan a través del intercambiador de calor.      Para los intercambiadores de calor, la ley de Newton del enfriamiento es     U : Coeficiente de transferencia de calor total A : Superficie de transferencia de calor D Tm : Diferencia de temperatura media Fig. 4.21 Intercambiadores de calor      Como el coeficiente U no es constante para todas las partes del intercambiador, conviene evaluarlo con base en la media aritmética de las temperaturas de los fluidos. Por analogía con la convección, se tiene 1/UA igual a la resistencia. La diferencia de temperatura media logarítmica se expresa como                                                                                                              Fig. 4.22 Otros intercambiadores de calor         El problema de calcular la transferencia de calor en los intercambiadores de calor, es que la temperatura de uno o ambos fluidos varía en forma continua a medida que los fluidos se transportan a través del intercambiador de calor. Esto puede observarse en la Figura 4.23, en la que se han trazado en forma gráfica las temperaturas del fluido como una función de la superficie de transferencia de calor para los casos mas comunes de flujo paralelo, contraflujo y para un fluido a temperatura constante. El subíndice h denota fluido caliente y el subíndice c, fluido frío. El subíndice 1 denota la temperatura a la entrada de un fluido al intercambiador de calor y 2 representa la temperatura del fluido a la salida del mismo. La dirección de flujo de cada fluido a través del intercambiador se muestra mediante flechas sobre las curvas de temperatura. La diferencia de temperatura mas grande entre los fluidos en la unidad (tanto a la entrada como a la salida) se designa como q A, y la diferencia de temperatura menor entre los fluidos (tanto a la entrada como a la salida) se designa como q B .                                                             Fig. 4.23 Temperatura de los fluidos en diferentes intercambiadores de calor

Ver también: PROBLEMAS RESUELTOS SOBRE CONDUCCIÓN

Ver también: PROBLEMAS RESUELTOS SOBRE CONVECCIÓN

Ver también: PROBLEMAS RESUELTOS SOBRE RADIACIÓN

Ver también: PROBLEMAS RESUELTOS SOBRE INTERCAMBIADORES DE CALOR

Ver también: PROBLEMAS RESUELTOS DE LA UNIDAD IV

Ver también: PROBLEMAS PROPUESTOSDE LA UNIDAD IV