UNIDAD II
|
|
PRIMERA LEY DE LA TERMODINÁMICA
Se llama también ley de la conservación de la energía.
PRIMERA LEY PARA UN SISTEMA QUE SIGUE UN CICLO
La primera ley para un sistema que cumple con un ciclo se define como:  donde Q viene expresado en kcaloría y W en kJoule; J es la constante de proporcionalidad y representa 0.2389 kJ/kcal.
Para entender mejor el significado de la ecuación, la Figura 2.13
muestra un sistema cerrado a volumen constante que cumple con un
ciclo, es decir va desde unas condiciones P1, T1 hasta unas condiciones
P2, T2 regresando nuevamente a las condiciones iniciales P1,T1.Durante
el ciclo se produce transferencia de calor y de trabajo.

Fig. 2.13. Sistema cerrado a volumen constante que cumple con un ciclo
Si se expresa tanto el calor como el trabajo en kJoule, la ecuación 2.5 se puede escribir de la siguiente forma: 
Esta ecuación dice simplemente que la suma de todos los calores es igual a la suma de todos los trabajos que atraviesan un sistema cuando éste cumple con un ciclo. Esta suma de calores y trabajos, debe hacerse en forma algebraica es decir, debe tomarse en cuenta los signos tanto de los trabajos como de los calores.
PRIMERA LEY PARA UN SISTEMA QUE CUMPLE CON UN CAMBIO
DE ESTADO
Energía almacenada en un sistema E:
Esta energía puede estar presente en una variedad de formas:
Energía Cinética: Debida al traslado de las moléculas. EC
Energía Potencial: Debida a las acciones mutuas de atracción o de
repulsión entre las moléculas. EP
Energía Interna: Esta asociada con la estructura interna de la materia. U
De esta forma se puede expresar la energía almacenada, como la suma
de la energía cinética, la energía potencial y la energía interna.
 Para enunciar la primera ley para un sistema que cumple con un cambio de estado, se considera el siguiente sistema mostrado en la Figura 2.14 
Fig. 2.14. Sistema cerrado que cumple con un cambio de estado.
El sistema mostrado en la Figura 2.14, posee inicialmente una energía almacenada E1, pero debido a una interacción con el medio exterior, el sistema es obligado a cambiar a otro estado en donde la energía almacenada es E2. Haciendo un balance de energía, se puede decir que la energía almacenada E2, debe ser igual a la suma de la energía almacenada E1 mas la energía que entra al sistema menos la energía que sale del sistema. Este balance se puede escribir de la siguiente forma:
Arreglando los términos

Observe que el signo negativo que acompaña al calor Qs,, es el signo que le corresponde por ser un calor que sale, mientras el signo negativo que acompaña al trabajo We , es el signo que le corresponde por ser trabajo que entra.
En general, la ecuación 2.9 se puede escribir como :

Esta ecuación corresponde a la primera ley para un sistema cerrado que cumple un cambio de estado. Cuando se haga la sustitución de los calores y los trabajos en las sumas, se debe tomar en cuenta la convención de signos escogida.
En la mayoría de los casos, las variaciones de la energía cinética y
potencial son despreciables, por lo que la ecuación de la primera ley se
puede expresar únicamente en función de la energía interna.

Tanto la energía almacenada E, como la energía interna U, son
propiedades y como tales se evalúan dentro del sistema. Tienen como
unidades las mismas unidades del calor y el trabajo pero no se evalúan
en los límites del sistema.
CALOR ESPECÍFICO
Cuando un sistema interacciona con el medio exterior cambiando su
temperatura de un valor T a otro T + dT, definimos el calor específico
como la capacidad calorífica que tiene el sistema de cambiar su
temperatura al suministrársele una cantidad de calor.

El calor específico es pues la cantidad de calor que es necesario
suministrar a la unidad de masa de un cuerpo para que su temperatura
aumente un grado. Las unidades para el calor específico son:
Si se expresa el calor específico en forma molar, las unidades para éste serán : 
El calor específico de sólidos y líquidos depende de la temperatura
pero no del tipo de transformación. En los gases además de depender de
la temperatura, depende del tipo de proceso experimentado al sufrir el
calentamiento. Se define de esta forma dos calores específicos para los
gases:
Calor específico a volumen constante: se obtiene midiendo el calor específico en un proceso a volumen constante 
Calor específico a presión constante: se obtiene midiendo el calor
específico en un proceso a presión constante

ENERGÍA INTERNA Y ENTALPÍA
La energía interna U de un fluido, como depende de su masa, es una
propiedad extensiva, y desempeña un importantísimo papel en la
termodinámica. Es una función de estado y, como tal, su variación global
cuando el fluido experimenta una transformación cíclica será nula:

Cuando un sistema cerrado interacciona con el medio exterior, ya sea
térmica o mecánicamente, su energía varía de acuerdo con el primer
principio (ecuación 2.11).
Puesto que el estado de un sistema es función de las variables P, V y
T, cualquier magnitud que sea función de estado queda determinada
unívocamente al conocer dos de dichos parámetros. Como la energía
interna es una función de ese tipo, se puede expresar de cualquiera de
las tres formas siguientes:
El desarrollo y evaluación de estas funciones para obtener valores de energía interna no es tan sencillo, por lo que resulta conveniente utilizar tablas de datos termodinámicos para distintas sustancias. Para determinar valores de energía interna específica u, se procede de la misma forma que se hizo para calcular el volumen específico. La entalpía es una función de estado que juega un trascendental papel en termodinámica. Al igual que la energía interna, la entalpía de una sustancia pura será función de dos parámetros de estado cualesquiera. Es una propiedad que se obtiene de combinar la energía interna, la presión y el volumen específico.
Consideremos un sistema, en un proceso en el que se mantiene
constante la presión, mientras se somete a un calentamiento. Fig. 2.15
 Fig. 2.15 Proceso Isobárico Aplicando la primera ley :
Como el proceso es a presión constante, el trabajo se puede expresar
como:
o lo que es lo mismo: Por ser la presión constante.
Sustituyendo en 2.17 se tiene la siguiente ecuación:
El término U+PV es lo que se denomina entalpía H y sus unidades son las de la energía. Por tanto, la ecuación 2.20 se puede escribir de la siguiente forma:
Es importante denotar, que aún cuando esta propiedad, fue determinada
a partir de un proceso isobárico, ésta se puede calcular en cualquier
estado, en función de las otras propiedades.
Tanto la energía interna, como la entalpía, se pueden expresar en
forma de valores específicos, dividiendo la propiedad extensiva entre la
masa.
 A partir de la ecuación de la primera ley en forma diferencial: se puede expresar el calor específico a volumen constante y a presión constante de la siguiente manera: 
EXPERIENCIA DE JOULE
El estudio de la energía interna tiene una importancia especial. Para ello es útil considerar la experiencia de Joule realizada en un dispositivo como el que se indica en la Figura 2.16. En el interior de un calorímetro perfectamente aislado del exterior se encuentra un baño de agua en equilibrio térmico con un sistema constituido por dos recipientes A y B de vidrio; el primero de ellos contiene una cierta masa de aire a la presión P y el segundo, en el que se ha hecho el vacío, se encuentra separado de aquél por un pequeño tubo que lleva una válvula incorporada. Cuando dicha válvula se abre, el gas fluye libremente de A hacia B hasta ocupar el volumen VA+VB. Joule no observó cambio en la temperatura del baño de agua y supuso que no se había transferido calor hacia o del aire. Puesto que tampoco se había efectuado trabajo, d W=0 y d Q=0, concluyó que la energía interna del aire no cambiaba aunque lo hicieran el volumen y la presión, es decir dU=0. Por consiguiente, pensó, que la energía interna es una función exclusiva de la temperatura y no de la presión o el volumen específico. (Joule demostró que para gases que se desvían significativamente del comportamiento de gas ideal, la energía interna no es sólo una función de la temperatura.) 
Fig. 2.16 Estudio de la variación de la energía interna de un gas en una
expansión libre. Experiencia de Joule.
Con la definición de la entalpía y la ecuación de estado de un gas ideal, se tiene 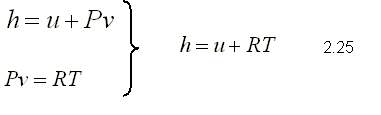
Puesto que R es constante y u=u(T), se deduce que la entalpía de
un
gas ideal es también sólo una función de la temperatura :
Como u y h sólo dependen de la temperatura en un gas ideal, los calores específicos Cv y CP dependen también, a lo sumo, sólo de la temperatura. Por consiguiente, a una temperatura dada u, h, Cv y CP de un gas ideal tienen valores físicos independientes del volumen o la presión específicos. Así que para gases ideales, las derivadas parciales en las ecuaciones 2.24 pueden sustituirse por derivadas ordinarias. Entonces los cambios diferenciales en la energía interna y la entalpía de un gas ideal se expresan como: 
El cambio en la energía interna o la entalpía en un gas ideal durante un
proceso del estado 1 al estado 2 se determina integrando estas
ecuaciones:
 Para realizar estas integraciones, es necesario tener las relaciones para Cv y CP como funciones de la temperatura.
A bajas presiones todos los gases se aproximan al comportamiento de
gas ideal y, por tanto, sus calores específicos dependen sólo de la
temperatura. Estos calores específicos suelen denotarse por CP0 y Cv0 .
Muchas veces en la solución de problemas se pueden considerar
constantes y se toman como calores específicos los valores leídos a
300 K.
RELACION DE CALORES ESPECIFICOS DE GASES IDEALES
Una relación especial entre CP y Cv se obtiene al diferenciar la relación lo que produce:
Al sustituir dh por CPdT u du por CvdT y dividir la expresión resultante
entre dT, se obtiene:
Esta es una importante relación para los gases ideales, porque permite determinar Cv a partir del conocimiento de CP y de la constante del gas R.
Esta expresión es válida para calores específicos molares, utilizando
como valor de R la constante universal
Otra propiedad importante para el gas ideal, es la llamada relación de
calores específicos k, definida como:

Si se despeja CP ó Cv de la ecuación 2.34 y se sustituye en la ecuación
2.33 se pueden obtener fácilmente las siguientes relaciones:

PROCESO ADIABATICO CUASI-EQUILIBRIO DE UN GAS IDEAL
Se considera un gas ideal
sometido a un proceso adiabático
cuasiequilibrio. Aplicando la primera ley en forma diferencial, se tiene lo
siguiente:
Como el proceso es adiabático, d Q=0. Si esta expresión se divide por la masa y el término d W se sustituye por su definición, la ecuación de la primera ley se puede escribir de la siguiente forma: Para gases ideales du=CvdT y P=RT/v  Dividiendo 2.39 por el producto CvT   integrando la ecuación 2.41 sustituyendo la ecuación de estado, se pueden obtener las siguientes expresiones 
La ecuación en función del volumen se puede expresar como volumen total y se puede evaluar entre dos estados eliminando así la constante  Estas relaciones permiten evaluar un proceso adiabático cuasiequilibrio de un gas ideal.
ECUACION DE TRANSPORTE
Es la ecuación utilizada para obtener las formulaciones de las ecuaciones básicas en un volumen de control. La ecuación de transporte representa una relación general entre la relación de cambio de cualquier propiedad extensiva arbitraria, Y, de un sistema y las variaciones de esta propiedad asociadas al volumen de control. La ecuación es la siguiente: 
Para deducir esta ecuación se hace una consideración importante que
consiste en hacer coincidir el sistema y el volumen de control. La
ecuación 2.46 relaciona la variación de cambio de cualquier propiedad
extensiva, Y, de un sistema con las variaciones de esta propiedad
asociadas al volumen de control, en el instante que coinciden el sistema
y el volumen de control. Para poder aplicar esta ecuación, es
conveniente comprender cada uno de los términos de la misma:

ECUACIÓN DE CONSERVACIÓN DE LA MASA
La ecuación de conservación de la masa es el primer principio físico al cual se le aplica la ecuación de transporte. Para obtener la ecuación se toma como propiedad extensiva la masa, es decir: y=m y y=1 . Al hacer la sustitución, se obtiene la siguiente ecuación:  Como la conservación de la masa establece que la masa de un sistema es constante, 
Sustituyendo 2.48 en 2.47, se llega a la ecuación de la conservación de la masa para un volumen de control:  En la ecuación 2.49, el primer término representa la relación de cambio de la masa dentro del volumen de control; el segundo término representa la relación neta de flujo que atraviesa la superficie de control.
Por otra parte, el producto punto:
Es positivo donde el flujo está hacia fuera de la superficie de control, negativo en el caso de que el flujo esté hacia dentro y cero cuando el flujo es tangente a la superficie de control. Esto se puede ver en la Figura 2.17. 
Fig. 2.17. Obtención de los signos para el producto de acuerdo al
sentido de los vectores en un volumen de control.
De acuerdo a lo anterior, el término de la entrada es negativo y el de la salida positivo. Simplificando la ecuación 2.49, se tiene lo siguiente:  
PRIMERA LEY PARA UN VOLUMEN DE CONTROL
Para obtener la primera ley, se sustituye como propiedad extensiva, Y=E y y=e que corresponden a la energía almacenada y la energía almacenada específica respectivamente. Para un sistema, la ecuación de la primera ley se puede escribir variando con respecto al tiempo como,  Sustituyendo la energía almacenada en la ecuación de transporte, (ecuación 2.46)  Sustituyendo 2.51 en 2.52    Sustituyendo 2.56 en 2.54:  Agrupando los términos de la superficie de control:     Considerando propiedades uniformes para el estado de las masas que cruzan la superficie de control a través de las secciones de entrada Ae y de salida As en cualquier instante: 
PROCESO DE FLUJO ESTACIONARIO
Antes de aplicar las ecuaciones de conservación de la masa y de primera ley al proceso de flujo estable, es indispensable conocer las características de este tipo de proceso. a) La masa del fluido dentro del volumen de control permanece constante es decir la masa que entra está exactamente compensada por la masa que sale de tal manera que no hay acumulación de masa dentro del volumen de control. b) El estado de la masa en cada punto del volumen de control es estacionario, es decir no varía con el tiempo. c) La energía transferida en los contornos del volumen de control, tanto en la forma de transferencia de calor como de trabajo se hace a una rata constante.
Las ecuaciones para este proceso de conservación de la masa y de
primera ley son:
Ecuación de conservación de la masa ya que no hay variación de la masa dentro del volumen de control
Ecuación de la Primera Ley

ya que no hay variaciones de las propiedades dentro del volumen de
control.
APLICACIONES DEL PROCESO DE FLUJO ESTACIONARIO
Se utiliza en el estudio de las plantas de vapor, plantas de gas, toberas y difusores, en los intercambiadores de calor y en una serie de máquinas de fluidos.
La tobera es un aparato que incrementa la velocidad de un fluido a
expensas de una caída de presión en la dirección del flujo.
El difusor es un aparato para incrementar la presión de una corriente
de flujo a expensas de un decrecimiento de velocidad.
PROCESO DE FLUJO TRANSITORIO
Sus características mas importantes son: a) El estado de la masa dentro del volumen de control puede variar con el tiempo pero en cualquier instante el estado es uniforme a través de todo el volumen de control. b) El estado de la masa que cruza cada una de las áreas de flujo sobre la superficie de control es constante con el tiempo. Ecuación de conservación de la masa o ecuación de continuidad. 
evaluando la ecuación para un intervalo de tiempo comprendido entre el
estado inicial y el estado final, tomando como t=0 el estado inicial y un
tiempo t cualquiera el estado final. Integrando

Ecuación de la Primera Ley
Integrando la ecuación 2.61  
APLICACIONES DEL PROCESO DE FLUJO TRANSITORIO
Este proceso se utiliza en el vaciado y llenado de recipientes, con o sin transferencia de calor, Figura 2.18. En la Figura 2.18-a se muestra un llenado de un recipiente sin transferencia de calor, mientras que la Figura 2.18-b corresponde a un vaciado de un recipiente con transferencia de calor. 
Fig.
2.18. Procesos de Flujo Transitorio
|

Ver también: PROBLEMAS RESUELTOS SOBRE TRABAJO Y CALOR PARA UN SISTEMA
Ver también: PROBLEMAS RESUELTOS SOBRE FLUJO TRANSITORIO
Ver también: PROBLEMAS RESUELTOS DE LA UNIDAD II
Ver también: PROBLEMAS PROPUESTOS DE LA
UNIDAD II
